AlphaGo とその後

2020年12月24日 2022年3月2日

gdep

AlphaGo とその後

北岡伸也氏
Dwango Media Village

1. はじめに

Google DeepMindによって開発されたコンピューター囲碁プログラムであるAlphaGo（アルファ碁）が、2016年３月のイベントで人間を超える強さを示したことは、大きな衝撃を持って世界に伝えられ、人工知能技術に注目をあつめる契機となりました。

しかし、AlphaGoに関連する技術が、そこから現在に至るまでにどのような進展をとげてきているかについて、よく知っている非専門家の方はそう多くないのではないでしょうか。

そこで、本稿ではAlphaGoから続く一連の技術がどのような過程を経て進化してきているか、5編の論文[1-5]を元に紹介していきたいと思います。

2. 最初のAlphaGo [1]

本稿で紹介するAlphaGoに連なる技術はすべてモンテカルロ木探索(MCTS; Monte-Carlo Tree Search)[6]と呼ばれるゲーム木探索の手法を基盤にしています。

囲碁は２人のプレイヤーが交互に着手することで盤面が進んでいくゲームですので、双方がどのような着手を選択するかで、現在の局面（ルート・根っこ）から次々と分岐の連なりができていきます。
この分岐の連なりが木のように見えることからゲーム木と呼ばれています。

AlphaGoが、どのような原理に基づいて動いているかを模擬的なゲーム木で図1に示しています。
ここではゲームのある局面を灰色の丸で表しています。そして、下方向に次の状態を展開していくように作図しているので、全体を見ると木を逆さにしたような形になっています。

局面を次々と展開して読みを深く入れることで、最もよさそうな応手の列（最善応手列：図では濃い灰色で示されている）を求め、現局面での最適な手を選択できるようにするというのが基本的な考え方になります。

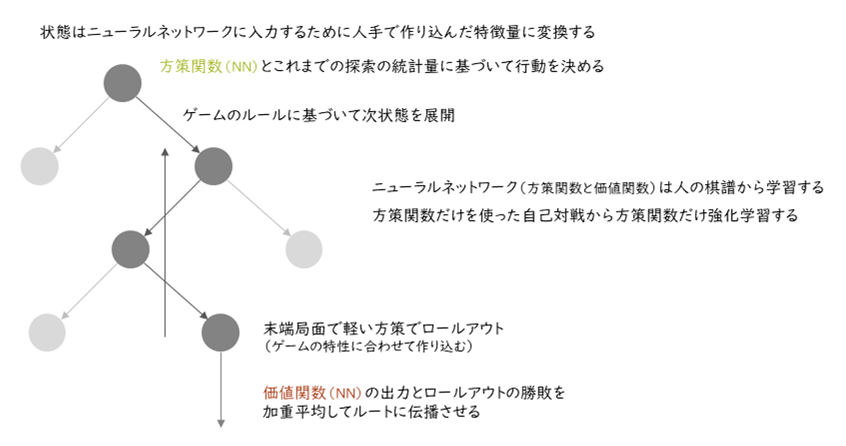
AlphaGoは、方策関数と状態価値関数という役割を担う2つのニューラルネットワーク[1]と、ロールアウト[2]と呼ばれるシミュレーション部分、そして囲碁のルールに基づいてニューラルネットワークへの入力を作ったり探索時のゲーム木を展開したりするプログラムで構成されています。

ニューラルネットワーク以外は、それ以前の囲碁プログラムでも同様の構成が使われていました。また、AlphaGo以前にもニューラルネットワークを囲碁プログラムに応用する研究は複数ありました[7, 8]。

AlphaGoが革新的であったのは、ニューラルネットワークに基づく技術を従来技術の枠組みの中で高いレベルで統合して、さらに強化学習（後述します）による棋力の向上に道筋を付けたことにあります。

■ ２つのニューラルネットワーク

AlphaGoで用いられている２つのニューラルネットワークは、それぞれ次のような役割を担っています。

方策関数（policy function）は、ゲーム木探索において読みを深くしていくための次の一手の候補を出力する機能を担っています。これにより膨大な着手候補から、もっともあり得そうな組み合わせを選択できるようになりました。従来技術では、この候補選択の精度が頭打ちになっており、探索の効率を上げられないという問題がありました。

状態価値関数（state value function）は、探索で見つけた局面がどれぐらい自分に有利かという大局観に相当する役割を担っています。従来技術では、ロールアウトによるシミュレーションのみを利用しており、それはプログラマーが職人芸的に作り込んでいた部分であったため設計が難しく、精度も十分ではない状況でした。

これらのニューラルネットワークは、人間が打った棋譜を元にしてパラメーターを最適化します。これにより、ニューラルネットワークの表現力も手伝って、従来と比較して圧倒的に精度の高い予測ができるようになりました。
またAlphaGoでは、ここからさらに強化するために方策関数の強化学習をしています。

■ 方策関数の強化学習

AlphaGoで使われている強化学習は、自己対戦を複数回繰り返した結果から、勝ちやすい手を選択できるようにニューラルネットワークの最適化を繰り返す手法を指しています。

最初に人間の棋譜の着手を真似るように学習してあるので、それだけを使って囲碁をプレイさせると、それなりの棋譜ができます。
その棋譜において勝った方の着手を選択するようにニューラルネットワークを更新し、再び囲碁をプレイされるとさらに洗練された棋譜ができます。そこからさらに――といったように反復させてどんどん強化できる手法になっています。

このような強化を囲碁でできるということを示したところがAlphaGoの革新的な点のひとつです。

1 本稿でいうニューラルネットワークは、計算機的に表現されたバックプロパゲーション可能な人工ニューラルネットワークを指す。
人間の脳のニューラルネットワークとはまったく関係ないことに注意。

2 バックギャモン（西洋すごろく）のAIで使われていた技術の応用で、サイコロを転がしてゲームの最終状態をシミュレーションすることからロールアウトという名前が付いている。囲碁ではサイコロを転がすわけではないので、プレイアウトと呼ばれることも多い。

■ 計算リソース

方策関数を構成するニューラルネットワークは、最初の人間の棋譜に基づいた最適化は50台のGPUによって3週間、つづく自己対戦による強化学習も50台のGPUによって1日で完了します。

価値関数を構成するニューラルネットワークは、人間の棋譜に基づいて50台のGPUにより1週間で最適化されます。対局時の構成は1,202台のCPUと176台のGPUでした。

3. AlphaGo Zero[2]とAlphaZero[3,4]

AlphaGoでは、ニューラルネットワークの作成の最初の段階で人間の棋譜を用いていました。
また、従来型の手作りでチューニングされたシミュレーション部を用いていました。

加えて、ニューラルネットワークへの入力も、囲碁についての人間の知識を反映できるように注意深く設計されていました。
たとえば、ここはコウになっているとか、このシチョウは取れる形、といったような情報が埋め込まれていました。
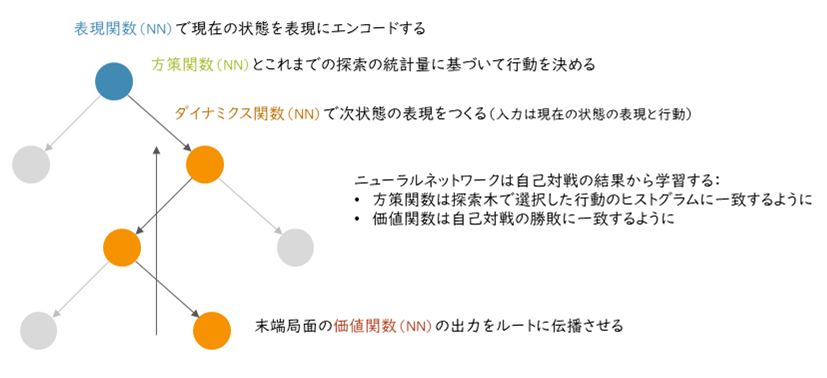
AlphaGo Zero は、これらの人手によるチューニングに依存した部分をなくして、ゼロから構成する手法を提案したものになります。

図2にAlphaGo Zeroの構成を示しています。AlphaGoにあった入力の特徴量変換部分や、ロールアウト部分がなくなっていることに注意してください。

■ ゼロからの学習

AlphaGo Zeroでは、人間の棋譜を使わずゼロからの強化学習のみで強くなっていきます。
AlphaGoの強化学習では方策関数だけを使って自己対戦と最適化を繰り返していました。
これに対してAlphaGo Zero はMCTSによる探索結果を活用して方策関数と価値関数の両方を同時に強化していく方法をとっています。

まず、ニューラルネットワークのパラメーターをランダムに初期化します。そのランダムなパラメーターを使ってMCTSにより自己対戦を行います。このとき、MCTSでよく探索された手を各局面で記録しておきます。また、最終的に勝ったか負けたか引き分けたかの結果も記録します。

次に、方策関数は、よく探索された手を再現できるように最適化し、状態価値関数は、その状態から終局時の結果を予測できるように最適化します。これらの自己対戦と最適化のステップを反復することで、どんどん強化していくという形式をとっています。

AlphaGoにはなかった探索を含めた自己対戦を用いていることで、対戦の精度が高くなり、ゼロからでも学習できるようになっています。

■ 計算リソース

探索を含めた自己対戦を行うため、計算リソースはAlphaGoのそれと比べても膨大になっています。

自己対戦と最適化はそれぞれ複数台のTPU (Tensor Processing Unit)を用いて40日ほどかけられています。
これがGPUに換算するとどれほどのリソースになるかということは、別の研究グループによって追試された結果[9, 10]から確認できます。

このときの計算資源は自己対戦に2,000台のGPU (4つのGPUあたり1つの Intel Xeon E5-2686v4プロセッサーが付いている)を使い、ニューラルネットワークのパラメーター最適化に8台のGPUを使用しています。いずれもNVIDIA Tesla V100です。

■ 任意のボードゲームへ

AlphaGo Zeroは、囲碁についての人間の知識を使わないように拡張されました。
つまり、任意のボードゲームについてAlphaGo Zeroの仕組みを適用できると言うことです。それを示したのがAlphaZeroであり、論文ではチェスと将棋についての結果が示されました。

また、このとき計算の効率化についても検討されており、自己対戦に5,000台のTPUを用い、最適化に64台のTPUを用いることで、24時間でAlphaGo Zeroを超える性能を達成しています。

4. MuZero[5]

AlphaZeroによってボードゲームであれば、そのゲーム専用の人間の知識なしでゼロから強化学習できるようになりました。

しかし、その探索部分は、ゲーム毎に局面の遷移をプログラミングする必要が依然としてありました。そのため、一般のゲームへ適用できないという問題がありました。そこで、この探索における状態の遷移自体もニューラルネットワークによって実現してしまおうというのがMuZero（ミュー・ゼロ）です。これにより、２人ゲームだけでない任意のビデオゲームに対応できるようになりました（論文中ではアタリ[1]の57ゲームで評価されています）。

図3にMuZeroの構成を示しています。方策関数と価値関数のほかに、表現関数とダイナミクス関数と呼ばれる２つのニューラルネットワークがあらたに加えられています。これらの役割については、MuZeroの学習の仕組みに沿って見ていくと理解しやすいと思います。

3 いわゆるアタリショックで知られるアタリ社のゲーム群。
シンプルで各種のゲームがそろっているので、強化学習の評価対象のゲームとしてよく用いられる。

■ あたらしいニューラルネットワーク

ダイナミクス関数（dynamics function）は、探索中のノード間の遷移を表現するニューラルネットワークです。
抽象的に表現された盤面の情報（実体としては実数の組として表現されます）と探索の中で選ばれた着手（行動）を入力として、次の状態の盤面の情報に相当する状態を出力する関数です。

表現関数（representation function)は、ダイナミクス関数で使われる抽象的な盤面の表現に、現在の盤面の状態（ビデオゲームであれば画面の画像そのもの）を変換するための関数です。
また、MuZeroでは方策関数と状態価値関数への入力もこの表現関数を通した結果が使われるように修正がされています。

■ 学習の仕組み

図4に、MuZeroの探索と学習の仕組みについて論文から引用した図を示します。

図4 (A)は、上記で示した探索の概念図を示しており、図4 (B)はAlphaZeroと同様の自己対局時の行動選択による遷移を表しています。
方策関数と価値関数をまとめた関数がf（function）で示されています：p（policy）が方策関数の出力でv（value）が価値関数の出力を表しており、その結果選択された着手がa（action）で示されています。

注目すべきは図4 (C)です。
表現関数hとダイナミクス関数gは、それ自体を直接的に最適化するのではなく、それを通して得られた状態を使って方策関数と状態価値関数の出力を得て、それが自己対戦の結果と一致するように最適化する方法をとっています。

また、ダイナミクス関数については探索で複数ステップ適用されることから、最適化時も複数ステップを通した結果で一致するように制約されています。

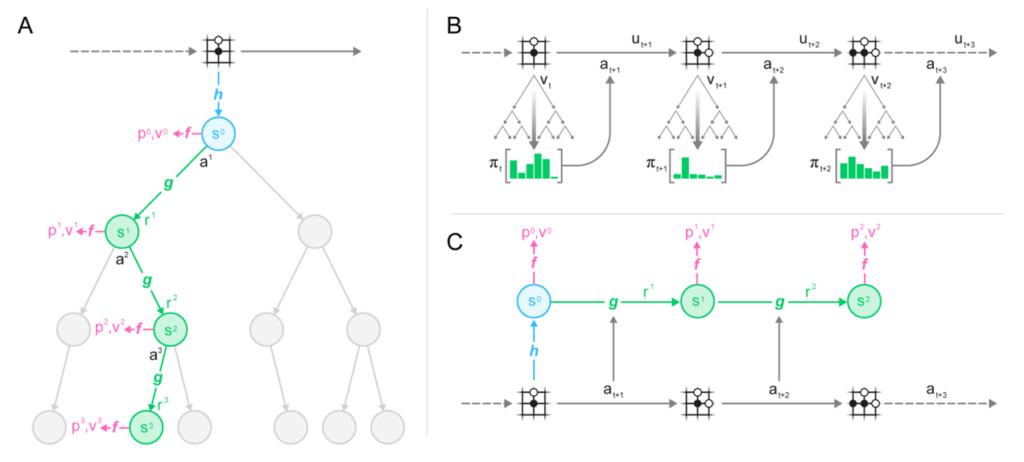
中間的な状態を明示的に設計するのではなく、選択する行動と状態の価値が一致するように抽象的な表現として獲得しています。

このようなゲーム内の状態の遷移ルールも含めてニューラルネットワークなどでモデル化しようとする技術は一般に世界モデル（World Models）[11]と呼ばれています。

これにより似た評価と行動になるような状態を同一の状態として表すような表現が獲得されているのではないかと考えられます。そのような効果によるところもおそらくあって、MuZeroでは、1,000台のTPUにより12時間でAlphaZeroと同等の強さに至るという、おおよそ10分の1程度の計算リソースの削減を達成しています（図5および図６）。

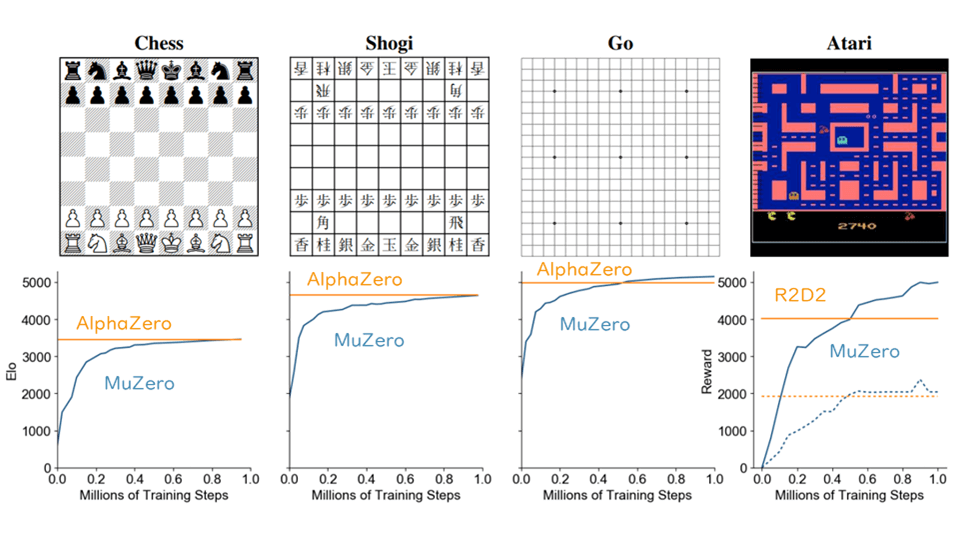
図 5: MuZeroのパフォーマンス（論文より引用）。
ビデオゲームの比較ではそのときの最高性能だったR2D2という手法との比較になっている
（ただしビデオゲームについては、すべての種類のゲームで上回っているわけではない）

図 6 計算リソースの比較。
AlphaZeroでは5,000TPUで24時間かかった計算が、
MuZeroでは1,000TPUを用いて12時間で実現できている（おおよそ10分の1の計算量）。

5. おわりに

MuZeroに至って、解きたい問題に依存するような人間の介在をなくすという取り組みがかなり成功しています。

今後もこのようにニューラルネットワークの応用で、まず大量のリソースでできる領域を広げつつ、次に省リソース化するという形で研究が進展していくのだろうと思います。

【参考文献】

[1] David Silver et. al. 2016. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484-489 (2016).
　　https://doi.org/10.1038/nature16961
[2] David Silver et. al. 2017. Mastering the game of Go without human knowledge. Nature 550, 354-359 (2017).
　　https://doi.org/10.1038/nature24270
[3] David Silver et. al. 2017. Mastering Chess and Shogi by self-play with a general reinforcement learning algorithm. arXiv:1712.01815.
　　https://arxiv.org/abs/1712.01815
[4] David Silver et. al. 2018. A general reinforcement learning algorithm that masters chess, shogi and Go through self-play.
  Science, Vol. 362, Issue 6419, pp. 1140-1144.
　　https://doi.org/10.1126/science.aar6404
[5] Julian Schrittwieser et. al. 2019. Mastering Atari, Go, Chess and Shogi by planning with a learned model. arXiv:1911.08265.
　　https://arxiv.org/abs/1911.08265
[6] Rémi Coulom. Efficient Selectivity and Backup Operators in Monte-Carlo Tree Search.
  5th International Conference on Computer and Games, May 2006, Turin, Italy. ffinria-00116992f
[7] Chris J. Maddison et. al. 2014. Move Evaluation in Go Using Deep Convolutional Neural Networks. arXiv:1412.6564.
　　https://arxiv.org/abs/1412.6564
[8] Yuandong Tian, Yan Zhu. 2015. Better Computer Go Player with Neural Network and Long-term Prediction. arXiv:1511.06410.
　　https://arxiv.org/abs/1511.06410
[9] Yuandong Tian, et. al. 2019. ELF OpenGo: An Analysis and Open Reimplementation of AlphaZero. arXiv:1902.04522.
　　https://arxiv.org/abs/1902.04522
[10] Yuandong Tian, et. al. 2019. ELF OpenGo: an analysis and open reimplementation of AlphaZero.
  Proceedings of the 36th International Conference on Machine Learning, PMLR 97:6244-6253, 2019.
　　http://proceedings.mlr.press/v97/tian19a.html
[11] David Ha and Jürgen Schmidhuber. 2018. World Models. arXiv:1803.10122.
　　https://arxiv.org/abs/1803.10122

著者紹介

北岡伸也氏

Dwango Media Village

2010年に大阪大学大学院情報科学研究科マルチメディア工学専攻を修了、博士（情報科学）。
現在は株式会社ドワンゴニコニコ事業本部 MLエンジニアリング部 (Dwango Media Village)
マルチメディア・エンジニアリング・セクションでマネージャーを務めている。
2017年度より人工知能学会の編集委員、2020年度より画像電子学会の編集理事。