GPUを用いた光害の可視化とその応用 ─ SIGGRAPH Asia発表論文解説

プロメテックCGリサーチ研究紹介
GPUを用いた光害の可視化とその応用
SIGGRAPH Asia発表論文解説
著者:土橋 宜典 先生 / 北海道大学 教授
1. はじめに
今回は、プロメテックCGリサーチの研究成果を解説します。
人工光源を考慮した夜空のレンダリングに関する研究で、コンピュータグラフィックス(CG)における世界最大の国際会議SIGGRAPH ASIA 2023で発表したものです[1]。
CGにおいて、空の表示は長く研究されてきた重要な課題の一つです。
リアルな空の色を計算するためには、大気を構成する微粒子による光の散乱現象を考慮しなくてはなりません。この計算には高次元の積分計算が含まれるため、長い計算時間を必要とします。
そのため、GPUを用いた並列計算に関する研究も盛んに行われています。
さて、この記事の内容は光害の可視化です。
光害というのは、夜間における過剰な人工光源によって生じる環境問題です。
夜空の明るさが増して星が見えにくくなる「天文光害」、生態系への悪影響を及ぼす「生態系光害」、人の生活リズムを乱す「健康影響」、不要な照明による「エネルギー浪費」など、さまざまな問題を生じます。光害は世界的な問題となっており、多くの研究が行われています[2]。
私たちは、天文光害に着目し、CGの観点からこの研究に取り組みました。
CGにおいては、日中または夕方に見られる青空や夕焼けの表示に着目したものばかりで夜空の可視化についてはほとんど研究例がありません。唯一といっていい研究例として、Jensenらのもの[3]がありますが、光害については考慮されていません。
光害の場合は、街灯やイルミネーションなど、膨大な数の人工光源を考慮しなくてはならず、計算量も膨大なものになります。
図1に示すように、ある視線方向に見える空の輝度を求めるには、視線上にサンプル点を発生し、各サンプル点での散乱光を積算する必要があります。そして、各サンプル点には数千個から数万個の人工光源からの光が到達します。そのため、そのまま計算したのでは、非常に長い計算時間がかかります。
私たちは、フーリエ変換とGPUによる並列計算を活用することで、この計算を数千倍から数万倍ほど高速化する方法を開発しました。
この方法について解説します。

2. 人工光源を考慮した夜空のレンダリング
この研究では、地形による遮蔽の影響は無視します。人工光源は、平野部に集中しているため、地形によって遮蔽される影響は少ないと考えられるためです。
人工光源を考慮した場合の夜空の輝度の計算式を説明します。観測点を原点とした極座標系を考えます(図2)。
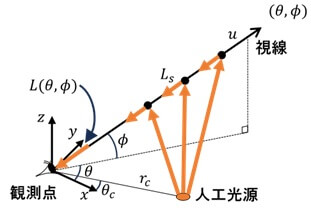
観測点からある方向 を見た時の空の輝度 は次の式で計算されます。
$$ L(\theta, \phi) = \int_0^R \int_0^{2\pi} L_c(r_c, \theta_c) r_c \left[ \int L_s(u) \, du \right] d\theta_c \, dr_c $$
(1)
ここで、\(L_{ c }(r_{c},\theta_{c})\)は観測点から距離\(r_{c}\) ,方位\(\theta_ {c}\)の位置にある人工光源の強度、\(L_{s}(u)\)はこの光源による視線上の一点での散乱光強度、\(u\)はその点と視点との距離を表します。つまり、内側の[ ]で囲まれた部分の積分は視線上の散乱光強度の総和を表し、外側の二つの積分は地形上の人工光源の総和を表しています。この3重積分を全ての視線方向について計算する必要がありますので、計算コストが極めて高いものになります。
上記の3重積分は視線方向ごとに独立に計算できるため、GPUによって視線ごとに並列に計算を行うことですが、それだけでは、インタラクティブに観測点の位置を変えながら可視化を行うといったことはできません。
3. 提案手法
私たちの方法のポイントは上式の内側の[ ]内の視線方向に関する積分を事前計算し、フーリエ変換を導入することです。
本節は少し専門的ですので、スキップいただいてもかまいません。
この内側の積分は観測点から人工光源までの距離\(r_{c}\) のみに依存します。そこで、人工光源の距離を様々に変更し、事前計算したデータの線形和として表します。すなわち、
$$ \int L_s(u) \, du \approx \sum_k c_k(r_c) B_k(\theta, \phi) $$
(2)
\(B_{k}(\theta,\phi)\)は基底分布と呼ばれるもので,主成分分析により求まります。\(c_{k}(r_{c})\)はその係数で,視点から人工光源の距離に依存します。この式を式(1)に代入すると次式のようになります。
$$ L_s(\theta, \phi) = \sum_k \int_0^{2\pi} H_k(\theta_c) B_k(\theta - \theta_c, \phi) \, d\theta_c $$
(3)
ただし、\(H_{k}(\theta_{c})\)は次式で与えられます。
$$ H_k(\theta_c) = \int_0^R L_c(r_c, \theta_c) c_k(r_c) r_c \, dr_c $$
(4)
さて、式(3)を見てなにかお気づきでしょうか。
この式は\(H_{k}\)と\(B_{k}\)の畳み込み(コンボリューション)になっているのです。つまり、式(3)はフーリエ変換を用いて高速に計算できます。
すなわち、以下の式で計算できます。
$$ L_s(\theta, \phi) = \sum_k \mathcal{F}^{-1} \left[ \mathcal{F}[H_k] \times \mathcal{F}[B_k] \right] $$
(5)
ここで、\(F\)および\(F^{-1}\)は、それぞれ、フーリエ変換・逆フーリエ変換を表します。
事前計算では、\(F[B_{k}]\) を求めておきます。この計算には時間がかかります。しかし、実行時には\(H_{k}\)を計算してそのフーリエ変換を行い、\(F[B_{k}]\)との乗算を行った後に、逆フーリエ変換を行います。
一見複雑に見えるかもしれませんが、高速フーリエ変換が利用できるため、数百倍の高速化が期待できます。そして、この計算を全てGPU上で実行することでさらなる高速化を図ります。
4. GPUによる並列計算
今回は、CUDAではなく、OpenGL Shading Language(GLSL)を使って並列計算を実装しました。必要なデータはすべてテクスチャとしてGPUメモリに転送します。図3に処理の流れを示しています。
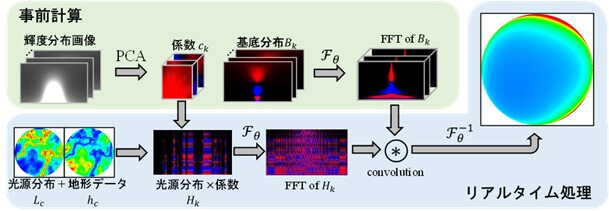
この方法では、入力データとして地形の高さマップと人工光源の分布を表す光源マップを使用します。これらは2次元テクスチャとしてGPUに転送しておきます。
また、事前計算したフーリエ変換後の基底分布\(F[B_{k}]\)と基底分布に対する係数\(c_{k}(r_{c})\)も同様にテクスチャとしてGPUに転送しておきます。ただし、これらは3次元テクスチャとして転送します。
以上の情報から、観測点位置での空の輝度分布をGPU上で計算します。
まず、式(3)の計算ですが、これは観測点からの距離\(r_{c}\)に関する積分ですが、上述の人工光源の分布と基底分布の係数\(c_{k}(r_{c})\)とをサンプリングして掛け合わせ、積和計算を行います。
その結果はテクスチャメモリに書き込みます。この計算は、方位\(_theta_{c}\) ごとに独立して計算が行えますので、並列に計算します。
その後、\(H_{k}(\theta_{c})\) の一次元フーリエ変換を行い、\(F[B_{k}]\)と\(F[H_{k}]\)の乗算とその逆フーリエ変換を計算します。
これらの計算もGPU上で実行します。計算結果は、GPUのテクスチャメモリ上に書き込まれ、そのまま空を表す半球ドームにマッピングして可視化されます。
5. 計算時間・精度の比較
計算時間と精度の比較を行います。
使用した計算機は、Intel Core i9 3.00 GHz(CPU)およびNVIDIA Quadro RTX 6000(GPU)を搭載したデスクトップパソコンです。
まずは、光が一回だけ散乱して視点に到達する一次散乱のみを考慮した手法での比較を行います。比較対象として、式(1)を視線ごとに並列計算する方法と私たちの方法を比較します。
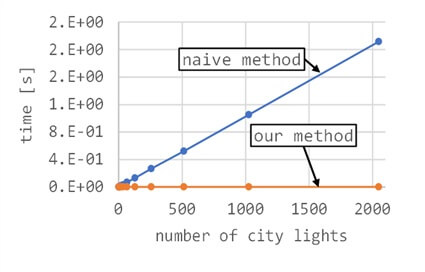
結果を図4に示しています。
このグラフは横軸が人工光源の数に相当し,縦軸は計算時間を表しています。式(1)をそのまま計算する方式では、光源数に比例して計算時間が増大しています。
光源数が2000個では、2秒もの時間がかかるため、インタラクティブに観測点の位置を変えるなどの操作は困難になります。2000個の光源数は決して多い方ではありません。
一方、私たちの開発した方法を用いると、光源数によらず、計算時間はほぼ一定で、2ms秒ほどです。私たちの方法により、1000倍ほど高速化が達成されています。
光源数が増加するとその差はさらに開いていきます。なお、平均的な計算誤差は0.3%ほどで私たちの方法による精度の低下は全く生じません。
次に、多重散乱および地形による遮蔽を考慮した場合との比較を行います。
参照画像は物理ベースのパストレーサMitsuba3[4]を用いて生成し、私たちの手法で計算した場合と比較します。
なお、Mitsuba3においてもGPUを用いた並列計算が行われています。
私たちの方法は地形による遮蔽を考慮していませんので、平均的な計算誤差は5%と大きくなってしまいました。
比較画像を図5に示します。
遮蔽の影響が大きい水平線付近で誤差が大きくなっています。しかし、視覚的には大きな違いは見られません。加えて、パストレーサを用いた参照画像では、ノイズが残っています。
計算時間については、参照画像の生成には130秒の時間がかかりますが、私たちの方法は先ほど同様2msしかかかりません。したがって,65,000倍ほどの高速化が達成されました。

6. インタラクティブな可視化システム
極めて高速な計算が実現できましたので、インタラクティブに光害を可視化するシステムを構築しました。
このシステムでは、順問題と逆問題の両方の観点から光害の影響を調べることができます。本システムの利用例としては、天体観測がまず挙げられます。
本システムを利用して暗い場所を探索し、観測に適した地点を見つけることができます。また、本システムは、都市の照明計画にも役立てることができます。
本システムでは、人工光源をインタラクティブに追加・削除できる機能や逆問題的に光害の影響を調査する機能を備えています。
以下のビデオは、これらの機能を実際に用いている様子を示しています。
7. おわりに
数学的な工夫とGPUを活用して多数の人工光源に照らされた夜空の画像を超高速に計算する研究を紹介しました。
この手法により、都市部の光環境を高速に可視化し、光害の影響をより正確に評価できるようになります。
今後はさらに計算精度を高め、異なる天候条件や地形の影響も考慮した解析を目指します。
人工光源による夜空の変化を理解することで、より持続可能な照明設計への指針を得ることもできるかもしれません。
参考文献・サイト
[1] Yoshinori Dobashi, Naoto Ishikawa, Kei Iwasaki, "Efficient Visualization of Light Pollution for the Night Sky," ACM Trans. on Graphics (Proc. SIGGRAPH Asia 2023), Vol. 42, No. 6, Article 219. https://doi.org/10.1145/3618337 [2] Fabio Falchi et al. ,The new world atlas of artificial night sky brightness.Sci. Adv.2,e1600377(2016). https://www.science.org/doi/10.1126/sciadv.1600377 [3] Henrik Wann Jensen, Frédo Durand, Julie Dorsey, Michael M. Stark, Peter Shirley, and Simon Premože. 2001. A Physically-Based Night Sky Model. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques -SIGGRAPH ’01 (2001). https://doi.org/10.1145/383259.383306 [4] Wenzel Jakob, Sébastien Speierer, Nicolas Roussel, Merlin Nimier-David, Delio Vicini, Tizian Zeltner, Baptiste Nicolet, Miguel Crespo, Vincent Leroy, and Ziyi Zhang. 2022. Mitsuba 3 renderer. https://mitsuba-renderer.org著者紹介

土橋 宜典 先生
北海道大学 大学院情報科学研究院 教授
プロメテックCGリサーチ 副所長
1992年 広島大学工学部卒業.1994年,同大大学院工学研究科博士課程前期修了.
1997年 同大博士課程後期修了.同年,広島市立大学情報科学部助手.
2000年 北海道大学大学院工学研究科 助教授.
2004年 同大大学院情報科学研究科 助教授.
2008年 同大大学院情報科学研究科 准教授.
2020年 同大大学院情報科学研究院 教授.工学博士.
主としてコンピュータグラフィックスに関する研究に従事.
Eurographics Best Paper Award,芸術科学会国際CG大賞特別賞,文部科学大臣表彰科学技術賞他.


