再サンプリングを利用した画像生成手法

1. はじめに

近年、CGによる画像生成手法として、パストレーシング(経路追跡法)を代表としたモンテカルロ法ベースの手法が広く使用されてきています。

モンテカルロ法ベースの手法は従来、1枚の画像を作成するのに数時間要するような映画やCMなどの映像制作向けのオフラインレンダリングにおいて用いられていましたが、最近ではゲームやVR向けのリアルタイムレンダリングにおいても主流となりつつあります。

モンテカルロ法ベースの手法では、光源から視点に到達する光のエネルギーを記述した寄与関数\(f\) を積分することで画像を生成します。

通常、この被積分関数\(f\) は複雑な関数であり、解析的に積分することが難しいため、モンテカルロ法を用いて積分値を推定します。

モンテカルロ法は、ある確率密度関数\(p\) に基づいて、サンプル\(x_i\) を大量に生成します。

サンプル\(x_i\)での関数値\(f(x_i)\) を確率密度\(p(x_i)\) で割った値\(f(x_i)/p(x_i)\) の期待値が、積分値\(I=∫f(x)dx\) と一致する性質を利用することで積分値 \(I\)を推定します。

このとき、被積分関数\(f\) になるべく比例した確率密度関数\(p\) を設計できれば、\(f(x_i)/p(x_i)\) の分散が少なく、少ないサンプル数でノイズの少ない画像を生成することができます。

しかしながら、そのような確率密度関数\(p\)を得ることは簡単ではありません。
これは、確率密度関数が正規化されている(積分値が1)必要があることと、サンプルの生成に確率密度関数\(p\)の不定積分とその逆関数が一般的に必要であることが原因です。

2. Resampled Importance Sampling

被積分関数\(f\)になるべく比例したサンプルを、なるべく簡易に生成する手法として、近年再サンプリング(resampling)に注目が集まっています。

再サンプリングを用いたモンテカルロ法ベースの画像生成法として、Resampled Importance Sampling (RIS)が2005年にTalbotらによって提案されています[1,2]。

RISでは、被積分関数\(f\)にそれほど比例していなくても、サンプルの生成が容易な確率密度関数\(p\) を用意します。

確率密度関数\(p\)を用いて\(M\)個の候補サンプル\(\{x_1,x_2,\ldots ,x_M\}\) を生成します。

次に、\(M\)個の候補サンプルの中から、1つのサンプルを再サンプリングします。

このとき、\(M\)個の候補サンプル\(\{x_1,x_2,\ldots ,x_M\}\) について重み\(\{w(x_1),w(x_2),\ldots ,(x_M)\}\) を計算しておき、重みに比例した確率で再サンプリングを行います。

RISでは、この重み\(w(x_i)\) として所望の関数\(\hat{q}(x_i)\) を候補サンプルを生成した確率密度関数 \(p(x_i)\)で割った値\(w(x_i)=\hat{q}(x_i)/p(x_i)\)を用いています。

そうすると、再サンプリングで得られたサンプルの分布は、所望の関数\(\hat{q}\)に近づくという性質が知られています。

図1に、RISの例を示します。

図1(a)が、サンプルの生成が容易な(すなわち不定積分の逆関数を比較的簡単に求められる)確率密度関数\(p\)を表しています。

図1(e)が、サンプルの生成が難しい所望の関数\(\hat{q}(x)\) に比例した確率密度関数\(q(x)=/ ∫\hat{q}(x)dx\)を表しています。

図1(b)から(d)が、RISによって再サンプリングされたサンプルの分布を表しており、それぞれ候補サンプル数\(M\)が2から16へと変化させています。

図1(b)から(d)を見て分かる通り、RISで生成されたサンプルの分布は、所望の確率密度関数\(q\) に近づいていることが見て取れます。

候補サンプルを生成する確率密度関数\(p\)が単純な単峰性でも、RISで生成されたサンプルは候補サンプル数\(M\)が2のときでも、所望の確率密度関数\(q\)のような双峰性になっていることがわかります。

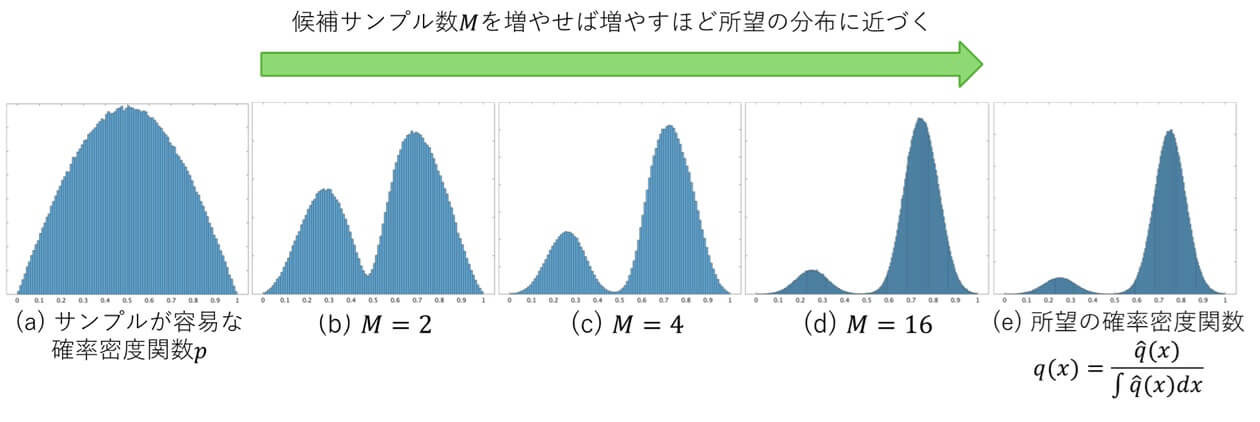
図2は、実際にRISを画像生成に適用した例になります。像の額付近でノイズが削減されていることが見て取れます。

左が従来の重点的サンプリングを用いた方法、
右がRISを用いた方法で、像の額付近でノイズが削減されていることがわかります。
*図は[1]より引用しています。

RISは、所望の関数\(\hat{q}\) が正規化されている必要がなく、サンプリングが難しいような分布でも、候補サンプル数\(M\) を大きくしていけば、所望の分布におおよそ従うサンプルを生成することができる強力な手法です。

しかしながら、RISに欠点がないわけではありません。
RISの欠点の一つとして、候補サンプル数\(M\)に比例したメモリ量が必要になるという点です。

再サンプリングをするためには、候補サンプルを格納しておく必要があります。画像生成では、各ピクセルで候補サンプルを格納しておく必要があるため、4Kなどの高解像度画像では候補サンプル数\(M\)を大きくすることは難しいと言えます。

また、重み\(w\)の計算量も候補サンプル数\(M\)に比例していますので、リアルタイムレンダリングのような時間の制限が厳しいアプリケーションでは、候補サンプル数\(M\)を大きくすることが難しいという問題があります。

3. ReSTIR

前述のRISの欠点を解決した手法が、2020年に発表された ReSTIR[3]という手法です。

ReSTIRは、Reservoir-based Spatio-Temporal Importance Resamplingの頭文字をとった略称で、リザーバを用いて時空間候補サンプルを再サンプリングする手法になります。
ReSTIRは、大量の光源からの直接照明を効率的にサンプリングするリアルタイムレンダリング向けの手法として開発されました。

ReSTIRでは、Weighted Reservoir Sampling (WRS)という手法[4]を用いて、候補サンプル数に比例したメモリ量を必要とするRISの欠点を解決しています。

そして、近傍ピクセルや隣接フレームでの候補サンプルの類似性を利用して、候補サンプルを再利用することで、重みの計算に時間を要するRISの欠点を解決しています。

WRSは、候補サンプル\(\{x_1,\ldots ,x_M\}\) を全て格納することなく、リザーバ(貯蔵庫)に少数(ReSTIRでは1つ)のサンプルを格納するだけで済む手法です。

WRSでは、候補サンプル\(x_i\) を一つ一つ順に処理していき、サンプルの重み\(w(x_i)\) によって計算される選択確率に基づいて、リザーバに格納されたサンプルと交換するか否かを決定します。

WRSの選択確率は、RISにおける候補サンプル\(\{x_1,\ldots ,x_M\}\) からサンプルを再サンプリングする確率と同じであることがミソです。

これにより、WRSのリザーバに格納されたサンプルが、RISによって再サンプリングされたことになります。

WRSでは、リザーバに格納されたサンプルと、処理したサンプルの重みの合計値、処理したサンプル数のみを格納すれば良いため、RISと比較して必要なメモリ量を大幅に削減することができます。

また、RISの様にあらかじめ候補サンプル数\(M\)を決めておく必要がなく、候補サンプルを順次追加していくことができます。そのため、近傍ピクセルのリザーバや隣接フレームのリザーバを統合することによって、候補サンプル数\(M\)を大幅に増やすことができます。

それによって、より所望の確率密度関数\(q\)に比例したサンプルを生成することができ、結果画像のノイズを大幅に削減することができます。

図3に、ReSTIRの結果画像を示します。
[Talbot 2005]と書かれた画像がRISを用いて生成した画像です。
RISを用いて生成した画像と比べて、ReSTIRではノイズを削減できていることがわかります。

RISと比較して、ReSTIRは省メモリ低コストで候補サンプル数を増やすことができるため、
同時間レンダリング(画像生成)において、モンテカルロ法によるノイズを大幅に削減できています。
*図は[3]より引用しています。

4. RISBPT

我々の研究グループでは、RISを双方向パストレーシング(Bidirectional Path Tracing)に応用した手法を提案しています[5]。

双方向パストレーシングとは、視点側と光源側の双方から経路をサンプリングします．サンプリングした経路を接続することで、光源から視点へ到達する経路を生成する手法です。

双方向パストレーシングでは、経路の接続によって同じ経路を複数重複してサンプリングしてしまう可能性があるため、重み関数というものを用いてこれを回避しています。

従来の双方向パストレーシングでは、単一の視点側経路と単一の光源側経路をサンプリングし、それぞれの経路頂点を問答無用に接続していたため、図4の様にシーン中の物体によって接続頂点間が遮られてしまい、光源から視点に到達する光のエネルギーが0の無駄な経路を生成してしまうという問題がありました。

我々の提案したRISベースの双方向パストレーシング(BPT)であるRISBPTでは、この問題を解決しています。

RISBPTでは、まず複数の光源側経路を生成します。
次に、視点側経路頂点において、サンプリングした光源側経路頂点をRISの候補サンプルとみなし、再サンプリングします。このとき、接続による寄与に比例した確率で経路を再サンプリングすることで、サンプリングされた経路の分布は、経路の寄与に比例した分布に近づいていきます。

RISBPTでは、双方向パストレーシングにおける経路の再サンプリングをRISとして解釈し、再サンプリングによって変化する確率密度に応じた重み関数を提案しています。

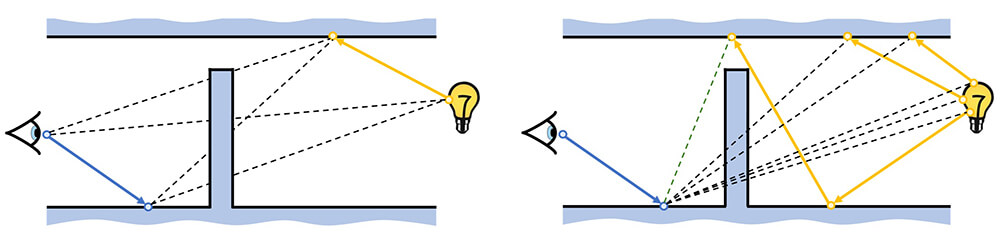
複数の光源側経路を用意し、再サンプリングによる接続を行うことで、
光源から視点に到達する経路をサンプリングすることができます。
RISBPTは光源側経路頂点の再サンプリングをRISと解釈し、
サンプリングされた経路の確率密度の変化を考慮した重み関数を導出しました。

図5に、RISBPTによる結果画像を示します。
RISBPTで提案された重み関数を用いることで、従来手法と比較してノイズを削減できていることがわかります。

前述した通り、RISでは候補サンプル数\(M\)を増やすほど所望の分布に近づくことができます。
RISBPTでも、光源側経路数を増やすことで、再サンプリングされた経路の分布は所望の分布に近づき、ノイズの削減が期待されます。
しかしながら、同時に重みの計算も増加してしまうという、RISと同じ欠点を共有しています。

この問題を解決するために、我々の研究グループではRISBPTを拡張し、２段階再サンプリングを用いた双方向パストレーシング法を提案しています[6]。

RISBPTと比較して、同時間で2桁多い数の光源側経路を扱うことができ、これにより平均絶対誤差率(Mean Absolute Percentage Error, MAPE)を最大2.3倍削減することを達成しています。

左は複数の光源側経路を用いた従来手法、右はRISBPT。
従来手法と比較して、RISBPTはノイズを削減できていることが
平均絶対誤差率(Mean Absolute Percentage Error, MAPE)と画像から見てとれます。

5. まとめ

本稿では、近年注目されている再サンプリングを用いた画像生成手法であるRIS、ReSTIR、RISBPTについて紹介しました。

ReSTIRは、大域照明に応用した手法[7,8]や、関与媒質に応用した手法[9]、半透明材質に応用した手法[10]など、様々な拡張・応用手法が発表されていますので、興味がある人はぜひ調べてみてください。

参考文献

[1] Justin F. Talbot, Importance Resampling for Global Illumination, Master Thesis. Brigham Young University, 2005.

[2] Justin F. Talbot, David Cline, Parris Egbert, Importance Resampling for Global Illumination, Proc. of Eurographics Symposium on Rendering, pp. 139—146, 2005.

[3] B. Bitterli, C. Wyman, M. Pharr, P. Shirley, A. Lefohn, W. Jarosz, Spatiotemporal Reservoir Resampling for Real-time Ray Tracing, ACM TOG, Vol. 39, No. 4, pp. 148:1—148:17, 2020.

[4] Min-Te Chao, A General Purpose Unequal Probability Sampling Plan, Biometrika, Vol. 69, No. 3, pp. 653—656, 1982.

[5] K. Nabata, K. Iwasaki, Y. Dobashi, Resampling-aware Weighting Functions for Bidirectional Path Tracing Using Multiple Light Sub-paths, ACM TOG, Vol. 39, No. 2, pp. 15:1—15:11, 2020.

[6] K. Nabata, K. Iwasaki, Y. Dobashi, Two-stage Resampling for Bidirectional Path Tracing using Multiple Light Sub-paths, Computer Graphics Forum (PG2020), Vol. 39, No. 7, pp. 219-230, 2020.

[7] Y Ouyang, S. Liu, M. Kettunen, M. Pharr, and J. Pantaleoni. ReSTIR GI: Path Resampling for Real-Time Path Tracing. Computer Graphics Forum, Vol. 40, No. 8, pp. 17—29, 2021.

[8] D. Lin, M. Kettunen, B. Bitterli, J. Pantaleoni, C. Yuksel, C. Wyman, Generalized Resampled Importance Sampling: Foundations of ReSTIR, ACM TOG, Vol. 41, No. 4, pp. 75:1—75:23, 2022.

[9] D. Lin, C. Wyman, C. Yuksel. Fast Volume Rendering with Spatio-temporal Reservoir Resampling, ACM TOG, Vol. 40, No. 6, pp. 278:1–278:18, 2021.

[10] M. Werner, V. Schubler, C. Dachsbacher, ReSTIR Subsurface Scattering for Real-Time Path Tracing, Proc. of the ACM on Computer Graphics and Interactive Techniques, Vol. 7, No.3, pp: 36:1—36:19, 2024.

著者紹介

1999年 東京大学理学部情報科学科卒業
2001年 同大学大学院新領域創成科学研究科博士前期課程修了
2004年 同大学大学院新領域創成科学研究科博士後期課程修了
同年      和歌山大学システム工学部情報通信システム学科助手
2007年 同講師
2009年 同准教授．科学博士．主としてコンピュータグラフィクスに関する研究に従事
2023年より現職